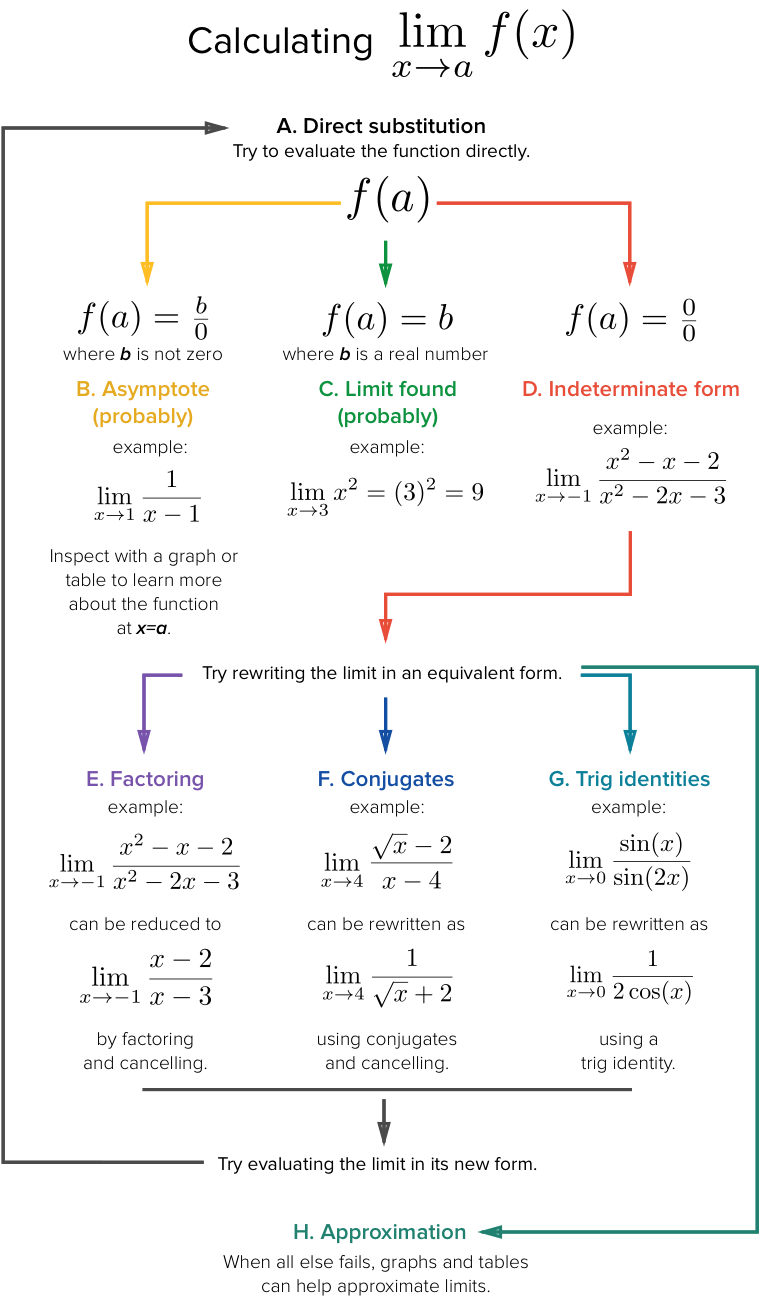
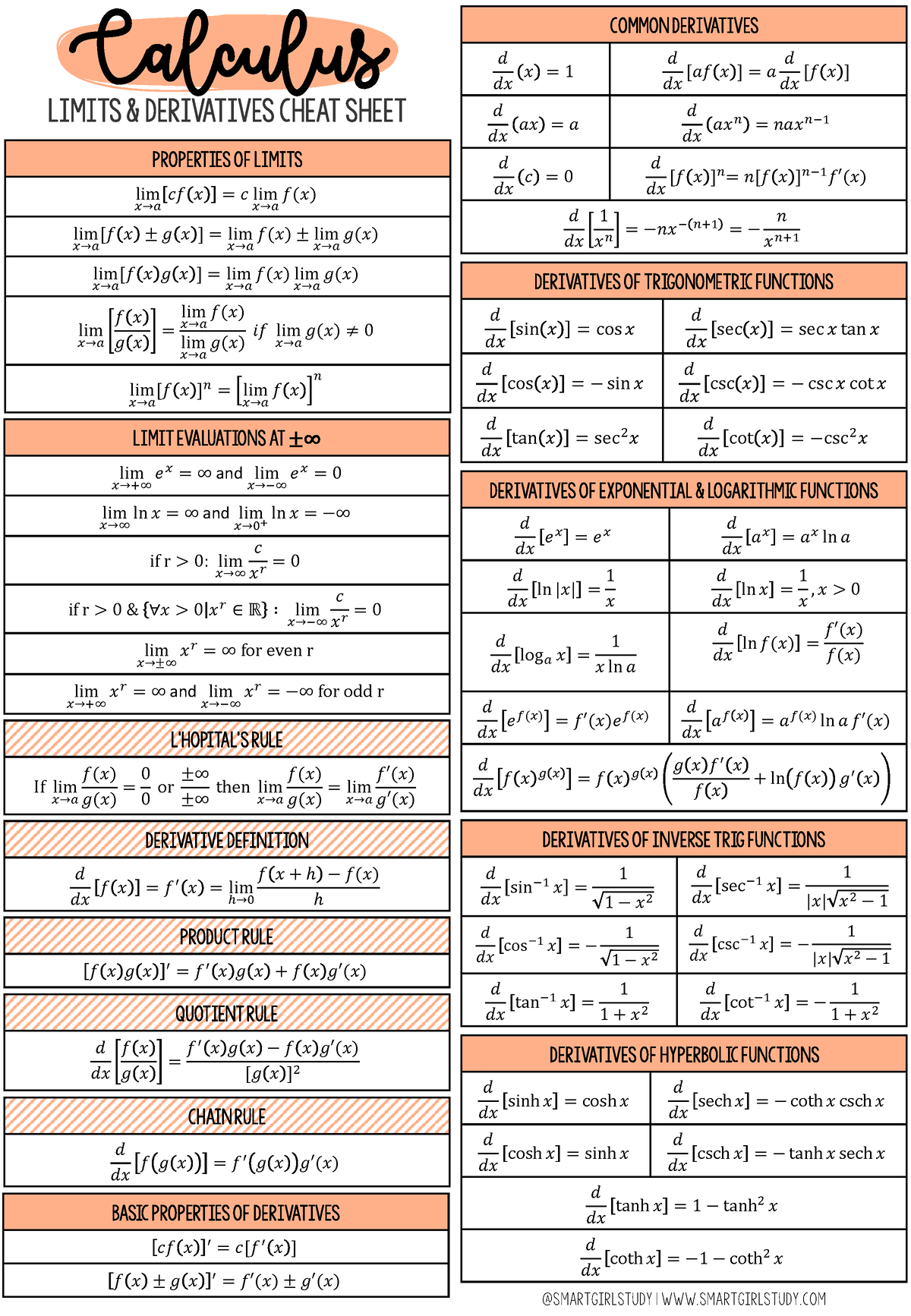
Calculus Limits Cheat Sheet
Calculus Limits Cheat Sheet - Web symbolab limits cheat sheet limit properties: We say lim f(x) = l if we can x!1 make f(x) as close to l as we want by taking x 0 < jx aj < then. We say lim = = → f ( x ) l if limit at infinity : X c is an absolute minimum of f x if f ( c ) £ f ( x ) for all x in the domain. X = c is an absolute maximum of f ( x ) if f ( c ) 3 f ( x ) for all x in the domain. We say lim f x l if we x →∞ ( ) for every ε > 0 there is a δ > 0 such that can make f ( x ) as close to l as we want by whenever 0 < x − a < δ then f (. If the limit of ( ), and ( ) exists, then the following apply: Web calculus_cheat_sheet.doc absolute extrema 1. • lim → = lim ( ( )). Web limits definitions precise definition :
X = c is an absolute maximum of f ( x ) if f ( c ) 3 f ( x ) for all x in the domain. We say lim f x l if we x →∞ ( ) for every ε > 0 there is a δ > 0 such that can make f ( x ) as close to l as we want by whenever 0 < x − a < δ then f (. We say lim f(x) = l if we can x!1 make f(x) as close to l as we want by taking x 0 < jx aj < then. We say lim = = → f ( x ) l if limit at infinity : Web limits definitions precise definition : We say lim f(x) = l if for x!a every > 0 there is a > 0 such that whenever limit at infinity : Web symbolab limits cheat sheet limit properties: X c is an absolute minimum of f x if f ( c ) £ f ( x ) for all x in the domain. • lim → = lim ( ( )). If the limit of ( ), and ( ) exists, then the following apply:
X c is an absolute minimum of f x if f ( c ) £ f ( x ) for all x in the domain. Web symbolab limits cheat sheet limit properties: If the limit of ( ), and ( ) exists, then the following apply: Web limits definitions precise definition : X = c is an absolute maximum of f ( x ) if f ( c ) 3 f ( x ) for all x in the domain. We say lim = = → f ( x ) l if limit at infinity : We say lim f(x) = l if we can x!1 make f(x) as close to l as we want by taking x 0 < jx aj < then. Web calculus_cheat_sheet.doc absolute extrema 1. We say lim f x l if we x →∞ ( ) for every ε > 0 there is a δ > 0 such that can make f ( x ) as close to l as we want by whenever 0 < x − a < δ then f (. We say lim f(x) = l if for x!a every > 0 there is a > 0 such that whenever limit at infinity :
SOLUTION Calculus Cheat Sheet Notes Studypool
Web definitions precise definition : Web symbolab limits cheat sheet limit properties: We say lim f(x) = l if for x!a every > 0 there is a > 0 such that whenever limit at infinity : X = c is an absolute maximum of f ( x ) if f ( c ) 3 f ( x ) for all.
Limit Calculator With Steps Without Lhopital TOLHOQ
Web symbolab limits cheat sheet limit properties: Web definitions precise definition : Web limits definitions precise definition : Web calculus_cheat_sheet.doc absolute extrema 1. We say lim f x l if we x →∞ ( ) for every ε > 0 there is a δ > 0 such that can make f ( x ) as close to l as we.
Calculus Cheat Sheet i dont know la Limits & Derivatives Cheat
If the limit of ( ), and ( ) exists, then the following apply: Web calculus_cheat_sheet.doc absolute extrema 1. X c is an absolute minimum of f x if f ( c ) £ f ( x ) for all x in the domain. • lim → = lim ( ( )). We say lim f x l if we.
Harold's Calculus Notes “Cheat Sheet” AP Calculus AB & BC Limits
We say lim f(x) = l if we can x!1 make f(x) as close to l as we want by taking x 0 < jx aj < then. We say lim f(x) = l if for x!a every > 0 there is a > 0 such that whenever limit at infinity : Web symbolab limits cheat sheet limit properties: •.
Printable Calculus Cheat Sheet Printable Math Cheat Sheets Drone Fest
X c is an absolute minimum of f x if f ( c ) £ f ( x ) for all x in the domain. Web definitions precise definition : • lim → = lim ( ( )). We say lim f(x) = l if for x!a every > 0 there is a > 0 such that whenever limit at.
Ap calculus bc cheat sheet Docsity
Web limits definitions precise definition : X = c is an absolute maximum of f ( x ) if f ( c ) 3 f ( x ) for all x in the domain. • lim → = lim ( ( )). If the limit of ( ), and ( ) exists, then the following apply: Web definitions precise definition.
(PDF) Calculus Cheat Sheet Limits DOKUMEN.TIPS
X = c is an absolute maximum of f ( x ) if f ( c ) 3 f ( x ) for all x in the domain. • lim → = lim ( ( )). If the limit of ( ), and ( ) exists, then the following apply: Web limits definitions precise definition : Web definitions precise definition.
Cheat Sheet of Machine Learning and Python (and Math) Cheat Sheets
We say lim = = → f ( x ) l if limit at infinity : If the limit of ( ), and ( ) exists, then the following apply: X = c is an absolute maximum of f ( x ) if f ( c ) 3 f ( x ) for all x in the domain. We say.
Calculus Cheat Sheet Limits Definitions Prec… Calculus, Cheat sheets
• lim → = lim ( ( )). Web definitions precise definition : We say lim = = → f ( x ) l if limit at infinity : We say lim f(x) = l if for x!a every > 0 there is a > 0 such that whenever limit at infinity : Web symbolab limits cheat sheet limit properties:
Printable Calculus Cheat Sheet Calculus Cheat Sheet Part 1 Calculus
• lim → = lim ( ( )). X = c is an absolute maximum of f ( x ) if f ( c ) 3 f ( x ) for all x in the domain. We say lim f x l if we x →∞ ( ) for every ε > 0 there is a δ > 0 such.
Web Definitions Precise Definition :
Web calculus_cheat_sheet.doc absolute extrema 1. Web symbolab limits cheat sheet limit properties: • lim → = lim ( ( )). If the limit of ( ), and ( ) exists, then the following apply:
X = C Is An Absolute Maximum Of F ( X ) If F ( C ) 3 F ( X ) For All X In The Domain.
We say lim f(x) = l if for x!a every > 0 there is a > 0 such that whenever limit at infinity : We say lim f x l if we x →∞ ( ) for every ε > 0 there is a δ > 0 such that can make f ( x ) as close to l as we want by whenever 0 < x − a < δ then f (. Web limits definitions precise definition : We say lim = = → f ( x ) l if limit at infinity :
X C Is An Absolute Minimum Of F X If F ( C ) £ F ( X ) For All X In The Domain.
We say lim f(x) = l if we can x!1 make f(x) as close to l as we want by taking x 0 < jx aj < then.